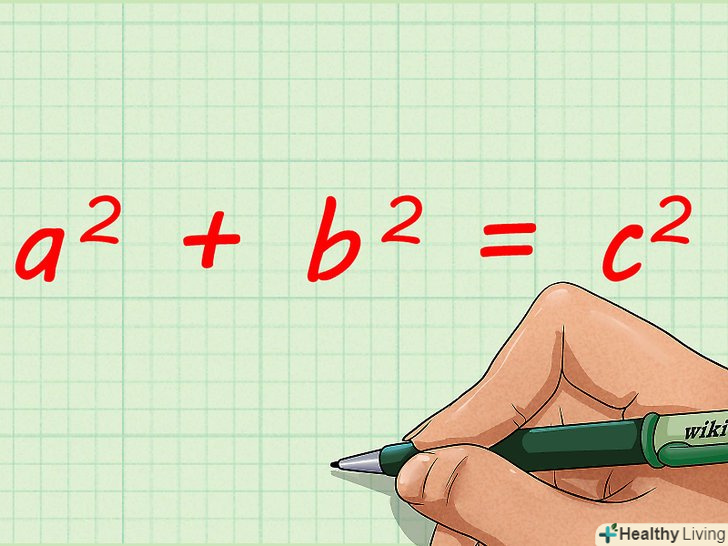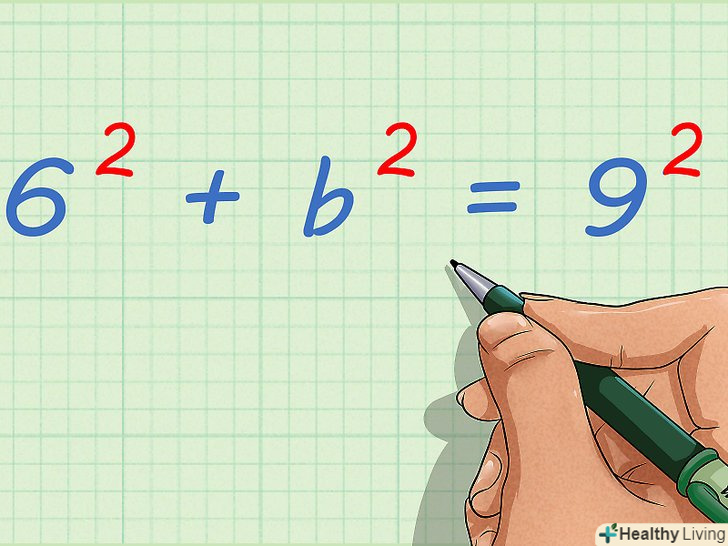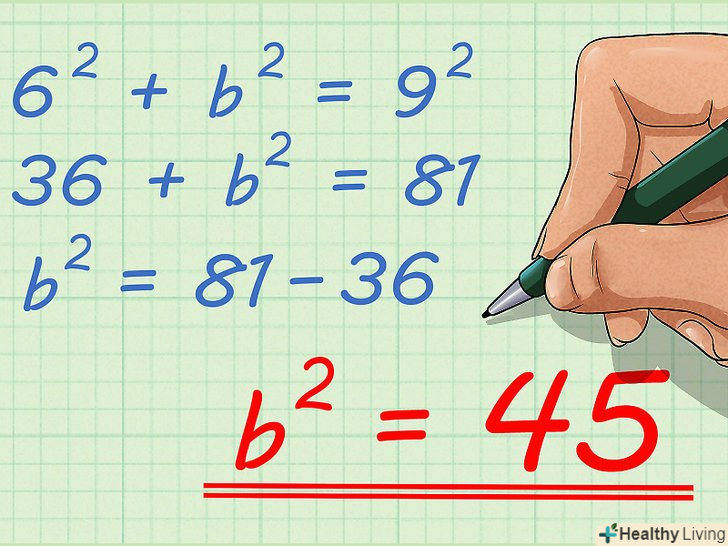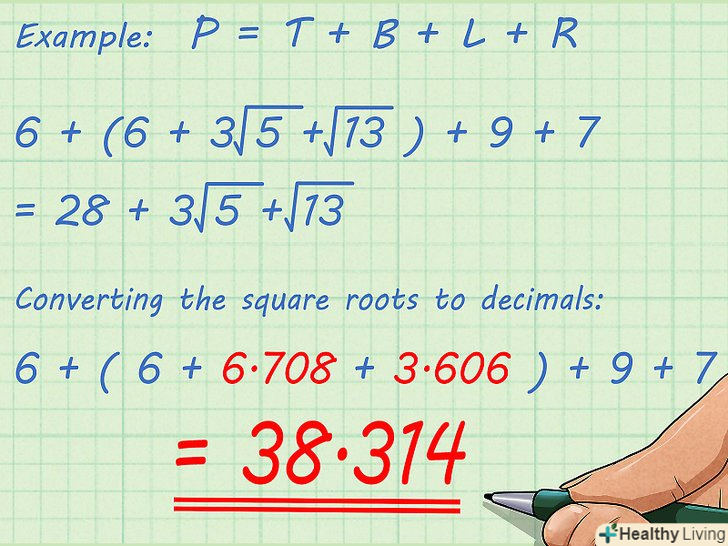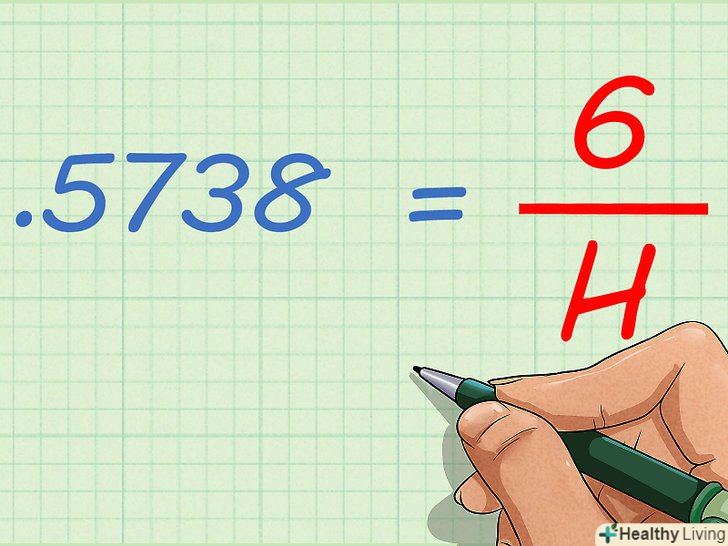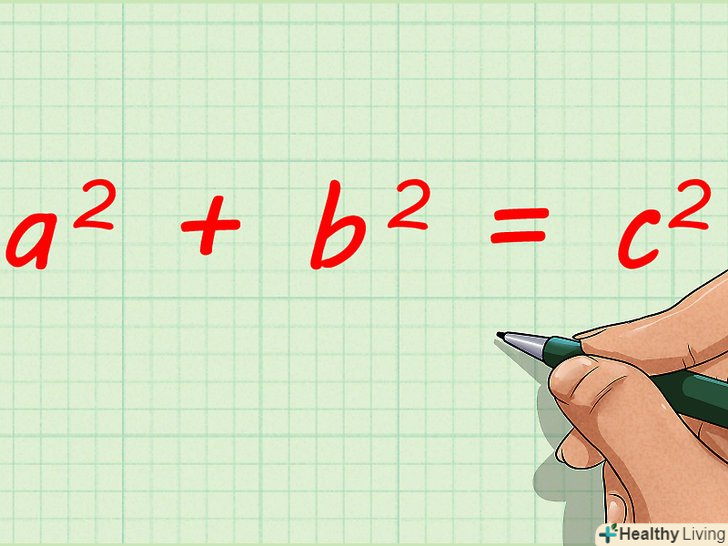Трапеція-це чотирикутник з двома паралельними сторонами. Щоб знайти периметр трапеції, потрібно скласти довжини всіх чотирьох сторін. Найчастіше в задачах довжини деяких сторін не дані, але відомі інші величини, наприклад, висота або кут трапеції. За допомогою відомих величин, а також геометричних і тригонометричних правил можна знайти невідомі сторони трапеції.
Кроки
Метод1З 3:
По відомих бічних сторонах і підставах
Метод1З 3:
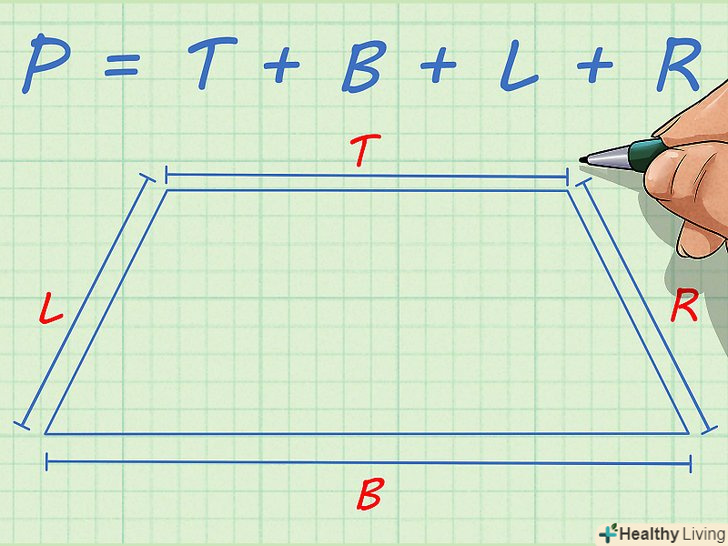
 Запишіть формулу для обчислення периметра трапеції. Формула:
Запишіть формулу для обчислення периметра трапеції. Формула:, де
– периметр,
– верхнє підставу,
– нижня основа,
– ліва бічна сторона,
– права бічна сторона.[1]
 У формулу підставте відомі довжини сторін. Не використовуйте цей метод, якщо не дано значення всіх чотирьох сторін.
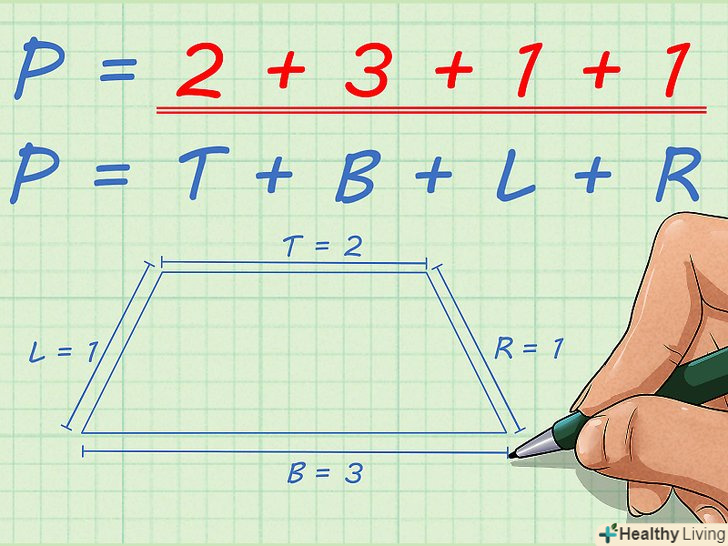
У формулу підставте відомі довжини сторін. Не використовуйте цей метод, якщо не дано значення всіх чотирьох сторін.- Наприклад, верхня основа трапеції дорівнює 2 см, Нижня основа дорівнює 3 см, а кожна бічна сторона дорівнює 1 см. У цьому випадку формула прийме наступний вигляд:
- Наприклад, верхня основа трапеції дорівнює 2 см, Нижня основа дорівнює 3 см, а кожна бічна сторона дорівнює 1 см. У цьому випадку формула прийме наступний вигляд:
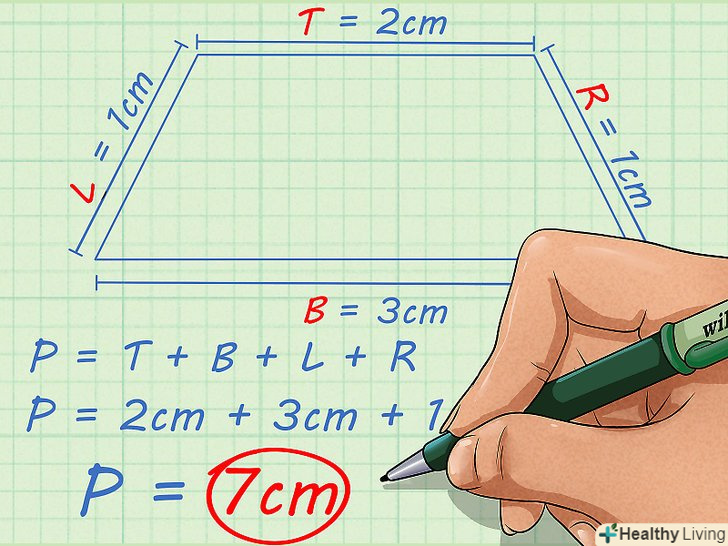
 Складіть довжини сторін.так ви знайдете периметр трапеції.
Складіть довжини сторін.так ви знайдете периметр трапеції.- У нашому прикладі:
Таким чином, периметр трапеції дорівнює 7 см
- У нашому прикладі:
Метод2 З 3:
По відомим висоті, боковим сторонам і верхній основі
Метод2 З 3:
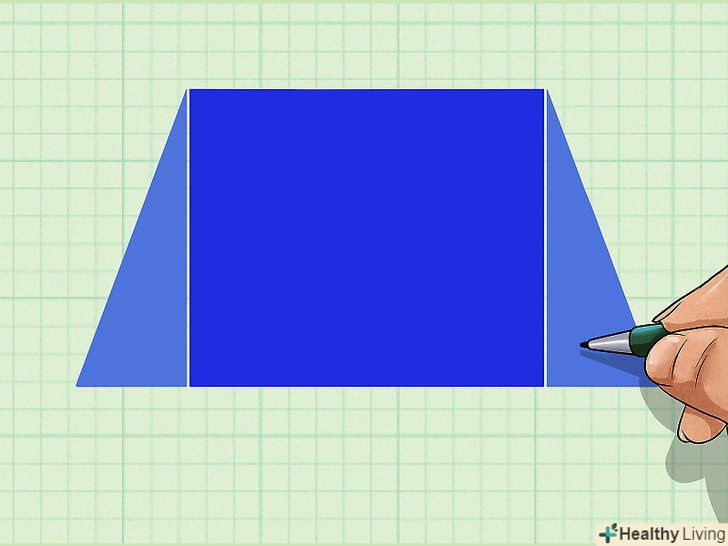
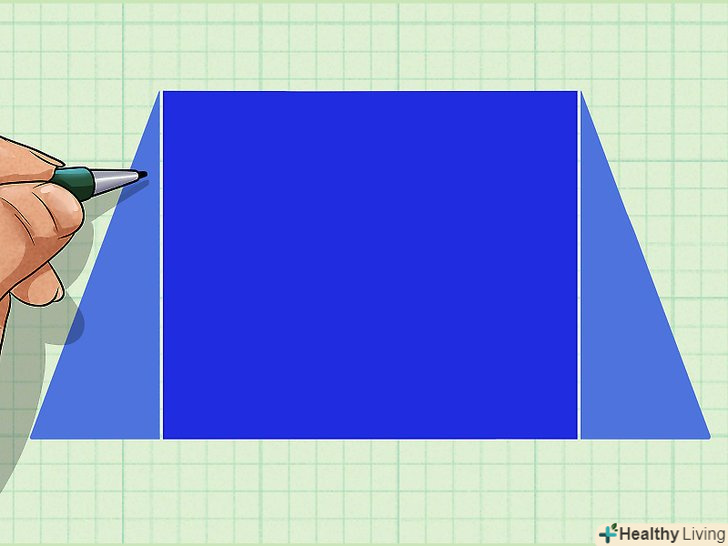
 Розбийте трапецію на прямокутник і два прямокутних трикутника.для цього з кожної вершини трапеції проведіть висоту.
Розбийте трапецію на прямокутник і два прямокутних трикутника.для цього з кожної вершини трапеції проведіть висоту.- Якщо одна сторона трапеції перпендикулярна підставам, ви не зможете отримати два прямокутних трикутника. У цьому випадку бічна сторона, перпендикулярна підставам, дорівнює висоті, а трапеція розбивається на прямокутник і один прямокутний трикутник.
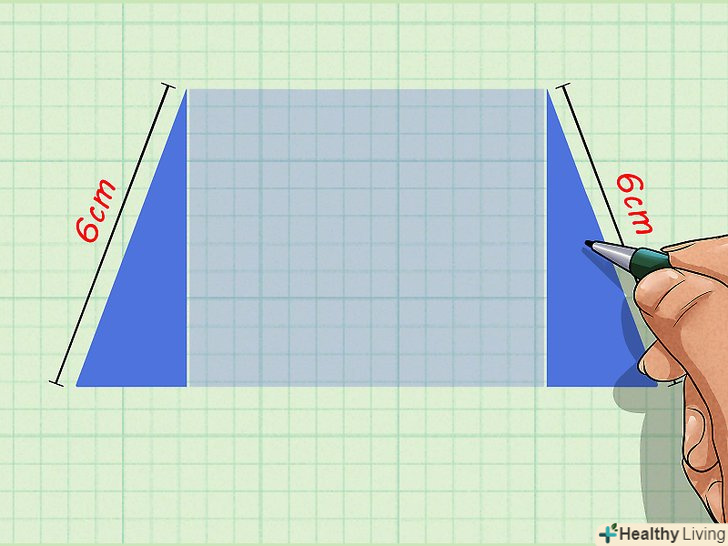
 Позначте кожну висоту.оскільки висоти є протилежними сторонами прямокутника, вони рівні.[2]
Позначте кожну висоту.оскільки висоти є протилежними сторонами прямокутника, вони рівні.[2]- Наприклад, висота трапеції дорівнює 6 см. з вершин трапеції проведіть дві висоти (до нижньої основи). Біля кожної висоти напишіть " 6 см "(без лапок).
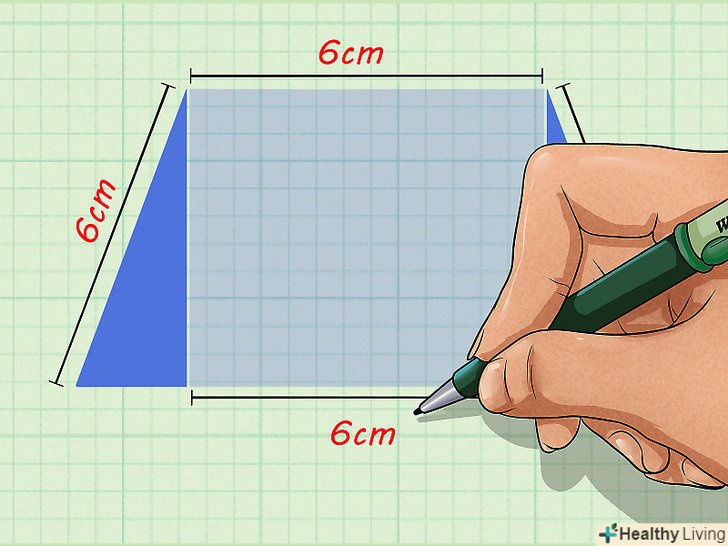
 Позначте середню частину нижньої основи (вона є нижньою стороною прямокутника). ця частина дорівнює верхній основі (тобто верхній стороні прямокутника), так як протилежні сторони прямокутника рівні.[3] не використовуйте цей метод, якщо не дано значення верхнього підстави.
Позначте середню частину нижньої основи (вона є нижньою стороною прямокутника). ця частина дорівнює верхній основі (тобто верхній стороні прямокутника), так як протилежні сторони прямокутника рівні.[3] не використовуйте цей метод, якщо не дано значення верхнього підстави.- Наприклад, якщо верхня основа трапеції дорівнює 6 см, то середня частина нижньої основи також дорівнює 6 см.
 Запишіть теорему Піфагора для першого прямокутного трикутника. Формула:
Запишіть теорему Піфагора для першого прямокутного трикутника. Формула:, де
– гіпотенуза трикутника (сторона, протилежна прямому куту),
– висота трикутника,
– основа трикутника.[4]
 У формулу підставте відомі величини першого трикутника. бічну сторону трапеції підставте замість
У формулу підставте відомі величини першого трикутника. бічну сторону трапеції підставте замість, а висоту трапеції підставте замість
.
- Наприклад, якщо висота трапеції дорівнює 6 см, а бічна сторона (гіпотенуза) дорівнює 9 см, то рівняння прийме наступний вигляд:
- Наприклад, якщо висота трапеції дорівнює 6 см, а бічна сторона (гіпотенуза) дорівнює 9 см, то рівняння прийме наступний вигляд:
 Зведіть в квадрат відомі значення. потім за допомогою віднімання відокремте змінну
Зведіть в квадрат відомі значення. потім за допомогою віднімання відокремте змінну.
- Наприклад, у рівнянні
зведіть в квадрат числа 6 і 9, а потім з 81 відніміть 36:
- Наприклад, у рівнянні
 Витягніть квадратний корінь, щоб знайти
Витягніть квадратний корінь, щоб знайти. (Щоб отримати інформацію про спрощення квадратних коренів, прочитайте цю статтю.) Ви знайдете основу першого прямокутного трикутника. Напишіть знайдене значення під підставою відповідного трикутника.
- У нашому прикладі:
Таким чином, під основою трикутника напишіть.
- У нашому прикладі:
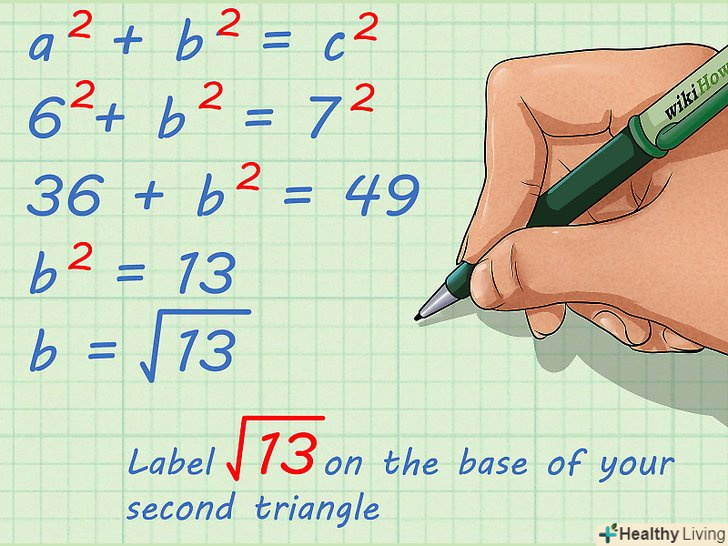
 Знайдіть невідому сторону другого прямокутного трикутника.для цього запишіть теорему Піфагора для другого трикутника і дійте так, як описано вище. Якщо дана рівнобедрена трапеція, у якій бічні сторони рівні,[5]то два прямокутних трикутника є рівними, тобто будь-яка сторона одного трикутника дорівнює відповідній стороні іншого.
Знайдіть невідому сторону другого прямокутного трикутника.для цього запишіть теорему Піфагора для другого трикутника і дійте так, як описано вище. Якщо дана рівнобедрена трапеція, у якій бічні сторони рівні,[5]то два прямокутних трикутника є рівними, тобто будь-яка сторона одного трикутника дорівнює відповідній стороні іншого.- Наприклад, якщо друга бічна сторона трапеції дорівнює 7 см, то формула запишеться так:
Таким чином, під основою другого трикутника напишіть.
- Наприклад, якщо друга бічна сторона трапеції дорівнює 7 см, то формула запишеться так:
 Складіть значення всіх сторін трапеції. Периметр будь-якого багатокутника дорівнює сумі всіх його сторін:
Складіть значення всіх сторін трапеції. Периметр будь-якого багатокутника дорівнює сумі всіх його сторін:. Нижня основа трапеції дорівнює сумі нижньої сторони прямокутника і підстав двох трикутників. В Інтернеті пошукайте інформацію про те, як складати квадратні корені, або просто скористайтеся калькулятором, щоб перетворити квадратні корені в десяткові дроби.
- У нашому прикладі:
Перетворивши квадратні корені в десяткові дроби, ви отримаєте:
таким чином, приблизний периметр трапеції дорівнює 38,314 см.
- У нашому прикладі:
Метод3 З 3:
По відомим висоті, підставах і нижніх кутах
Метод3 З 3:
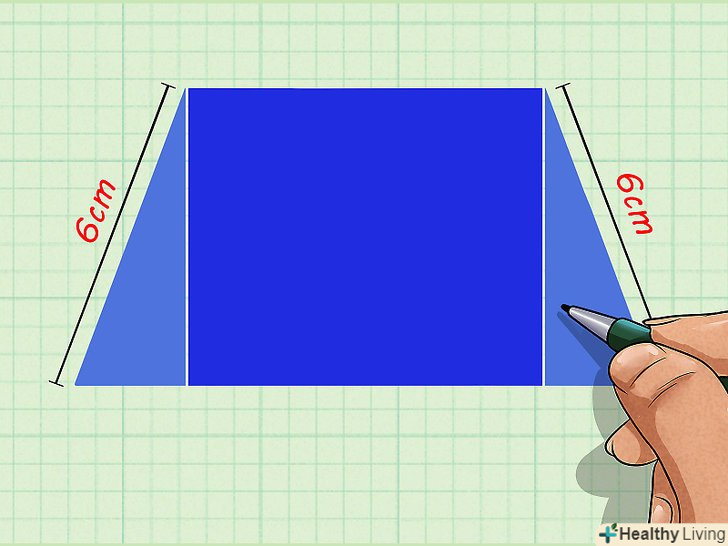
 Розбийте трапецію на прямокутник і два прямокутних трикутника.для цього з кожної вершини трапеції проведіть висоту.
Розбийте трапецію на прямокутник і два прямокутних трикутника.для цього з кожної вершини трапеції проведіть висоту.- Якщо одна сторона трапеції перпендикулярна підставам, ви не зможете отримати два прямокутних трикутника. У цьому випадку бічна сторона, перпендикулярна підставам, дорівнює висоті, а трапеція розбивається на прямокутник і один прямокутний трикутник.
 Позначте кожну висоту.оскільки висоти є протилежними сторонами прямокутника, вони рівні.[6]
Позначте кожну висоту.оскільки висоти є протилежними сторонами прямокутника, вони рівні.[6]- Наприклад, висота трапеції дорівнює 6 см. з вершин трапеції проведіть дві висоти (до нижньої основи). Біля кожної висоти напишіть " 6 см "(без лапок).
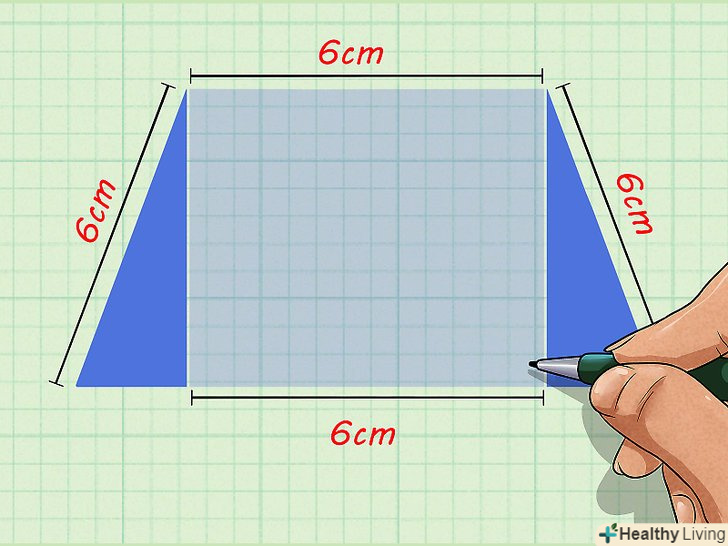
 Позначте середню частину нижньої основи (вона є нижньою стороною прямокутника). ця частина дорівнює верхній основі (тобто верхній стороні прямокутника), так як протилежні сторони прямокутника рівні.[7]
Позначте середню частину нижньої основи (вона є нижньою стороною прямокутника). ця частина дорівнює верхній основі (тобто верхній стороні прямокутника), так як протилежні сторони прямокутника рівні.[7]- Наприклад, якщо верхня основа трапеції дорівнює 6 см, то середня частина нижньої основи також дорівнює 6 см.
 Напишіть функцію (формулу) синуса кута першого прямокутного трикутника. Функція:
Напишіть функцію (формулу) синуса кута першого прямокутного трикутника. Функція:, де
– нижній кут трапеції,
– протилежна (кут) сторона трикутника,
– гіпотенуза.
- За допомогою функції синуса можна знайти гіпотенузу трикутника, Яка є бічною стороною трапеції.
- Гіпотенуза-це сторона, протилежна прямому куту трикутника.
 У формулу синуса підставте відомі величини.замість протилежної сторони підставте висоту трикутника. Ви знайдете гіпотенузу, тобто бічну сторону трапеції.
У формулу синуса підставте відомі величини.замість протилежної сторони підставте висоту трикутника. Ви знайдете гіпотенузу, тобто бічну сторону трапеції.- Наприклад, якщо нижній кут трапеції дорівнює 35 градусів, а висота трикутника дорівнює 6 см, то формула запишеться так:
- Наприклад, якщо нижній кут трапеції дорівнює 35 градусів, а висота трикутника дорівнює 6 см, то формула запишеться так:
 Знайдіть синус кута.це робиться за допомогою наукового калькулятора, а саме клавіші SIN. Знайдене значення підставте в формулу.
Знайдіть синус кута.це робиться за допомогою наукового калькулятора, а саме клавіші SIN. Знайдене значення підставте в формулу.- За допомогою калькулятора ви знайдете, що синус кута в 35 градусів приблизно дорівнює 0,5738. Таким чином, формула прийме наступний вигляд:
- За допомогою калькулятора ви знайдете, що синус кута в 35 градусів приблизно дорівнює 0,5738. Таким чином, формула прийме наступний вигляд:
 Знайдіть змінну H. для цього кожну сторону рівняння (формули) помножте на Н, а потім кожну сторону рівняння розділіть на синус кута. Або просто розділіть висоту трикутника на синус кута.
Знайдіть змінну H. для цього кожну сторону рівняння (формули) помножте на Н, а потім кожну сторону рівняння розділіть на синус кута. Або просто розділіть висоту трикутника на синус кута.- У нашому прикладі:
Таким чином, гіпотенуза, тобто бічна сторона трапеції, приблизно дорівнює 10,4566 см.
- У нашому прикладі:
 Знайдіть гіпотенузу другого прямокутного трикутника. напишіть функцію (формулу) синуса кута другого прямокутного трикутника:
Знайдіть гіпотенузу другого прямокутного трикутника. напишіть функцію (формулу) синуса кута другого прямокутного трикутника:. Так ви знайдете гіпотенузу другого трикутника, Яка є другою бічною стороною трапеції.
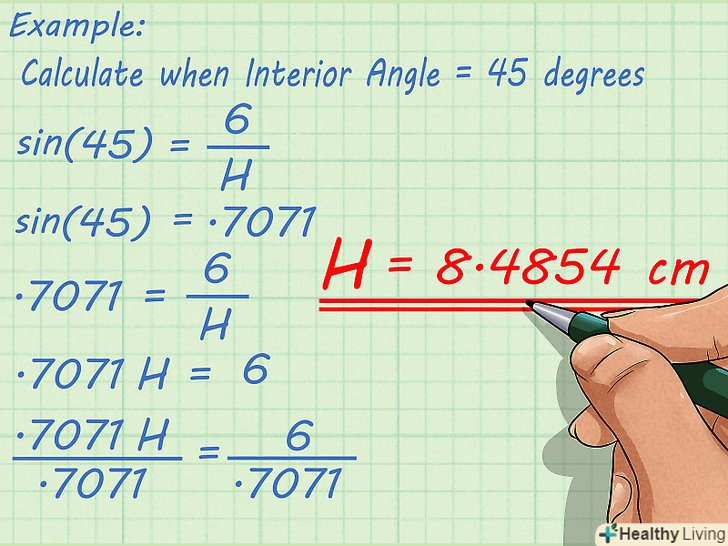
- Наприклад, якщо другий нижній кут трапеції дорівнює 45 градусів, то обчислення будуть наступними:
Таким чином, гіпотенуза, то є друга бічна сторона трапеції, приблизно дорівнює 8,4854 см.
- Наприклад, якщо другий нижній кут трапеції дорівнює 45 градусів, то обчислення будуть наступними:
 Запишіть теорему Піфагора для першого прямокутного трикутника. Формула:
Запишіть теорему Піфагора для першого прямокутного трикутника. Формула:, де